满足不同场景知识变现服务需求
知识付费解决方案:
无需开发,全网打通,一键搭建专属知识店铺
多端支持
支持微信公众号、微信小程序、APP、PC网页
品牌塑造
界面自定义装修设计、打造个人品牌知识店铺
变现闭环
满足获客-运营-转化-管理全链路闭环经营的需求

了解详情
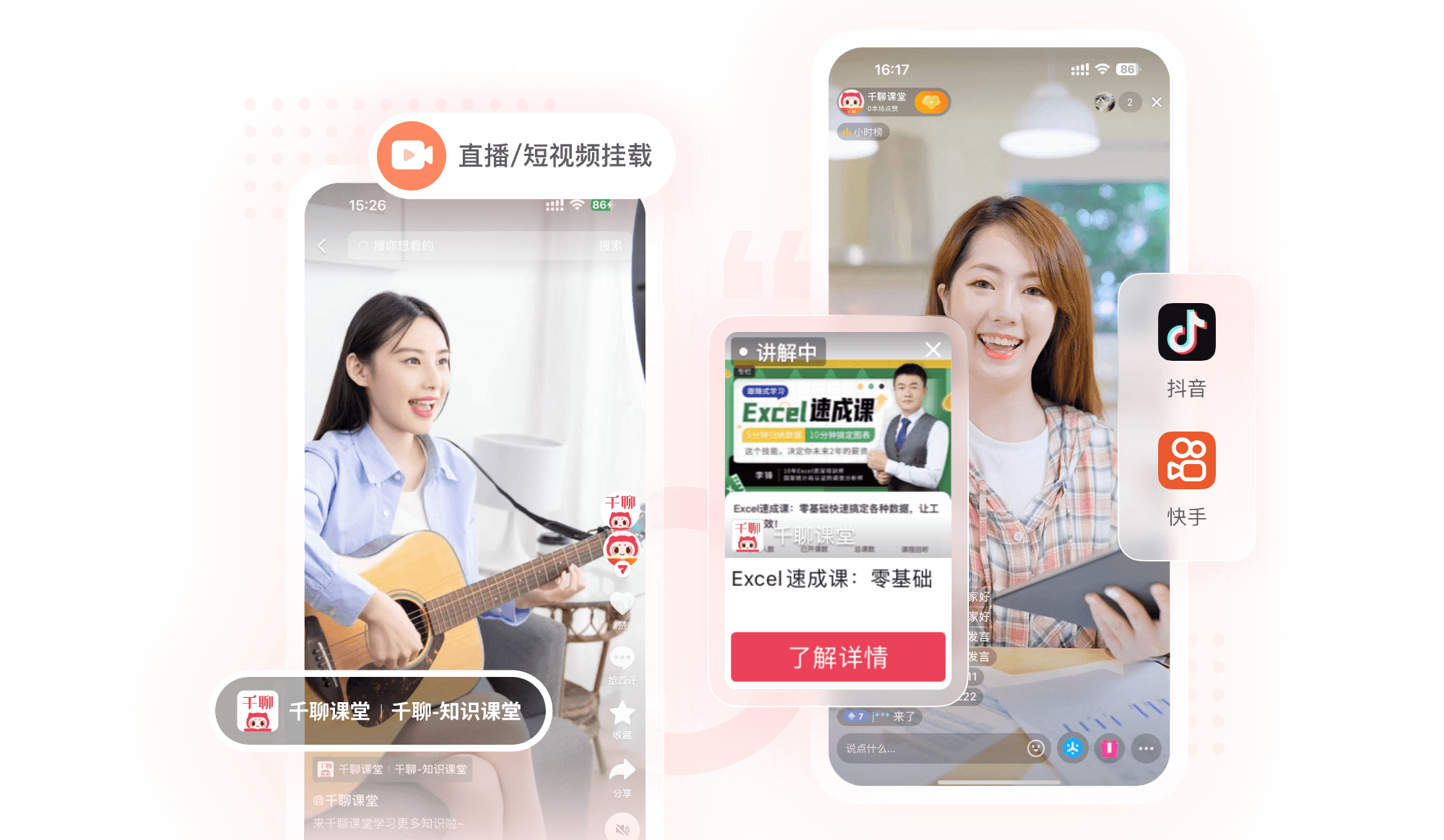
抖音快手卖课解决方案:
链接数亿公域流量,打造抖快知识变现场景
多形式挂载
短视频/直播间一键挂载,抖音快手内实现课程交付
超短链路
无需跳转其他APP,从“浏览”到“下单”一步完成
无资质要求
不同于其它平台的注册、审核流程,只需一键注册知识店铺,上传课程,即可实现挂载推广
了解详情
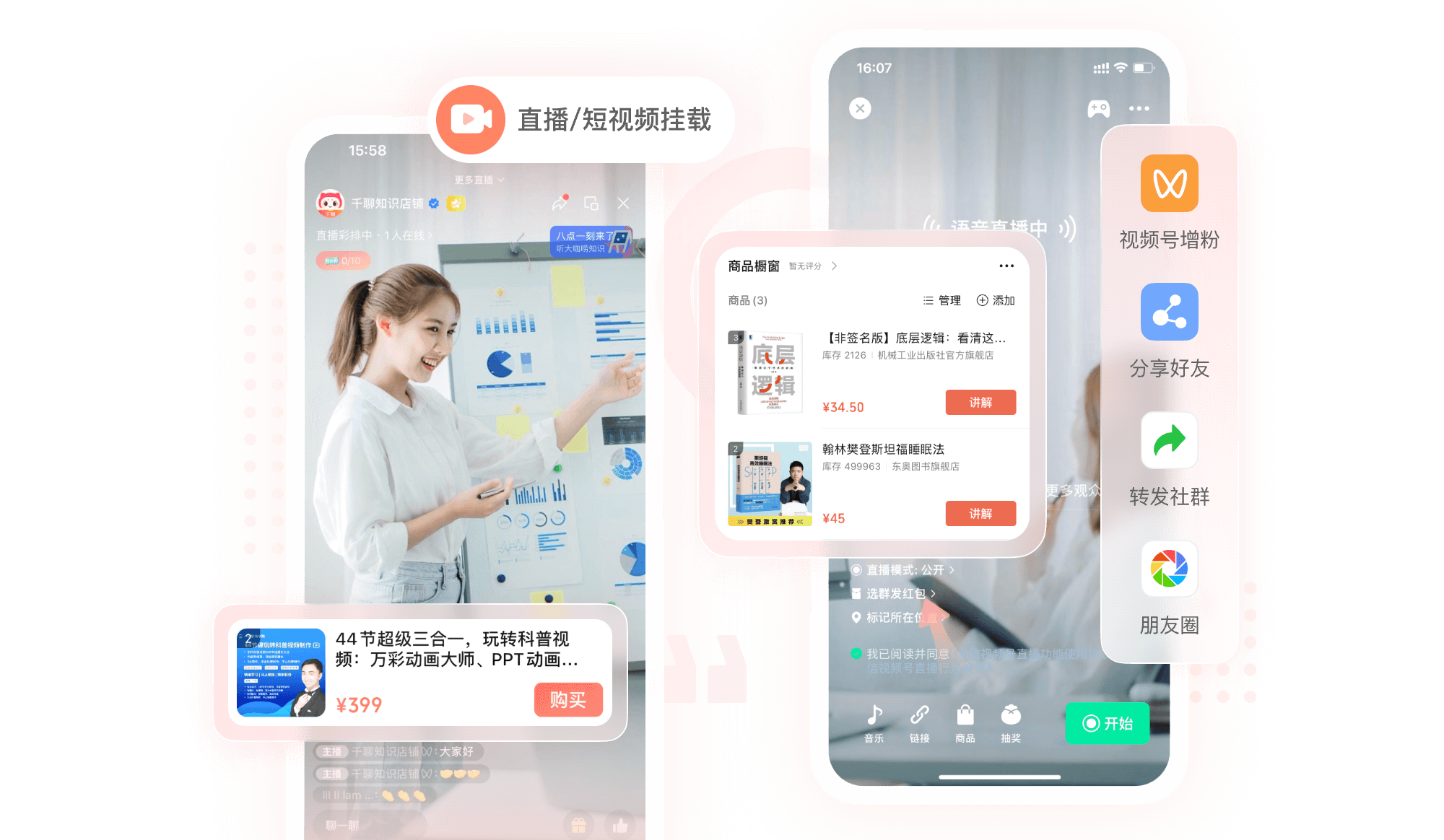
视频号卖课解决方案:
链接12亿微信生态流量,打造视频号知识变现场景
多形式挂载
短视频/直播间一键挂载,视频号内实现课程交付
0门槛入驻
无需ICP备案、无需保证金和类目资质审核
自动分销
直达选品中心,其它视频号创作者与学员也能进行分销,助力创作者内容变现
了解详情
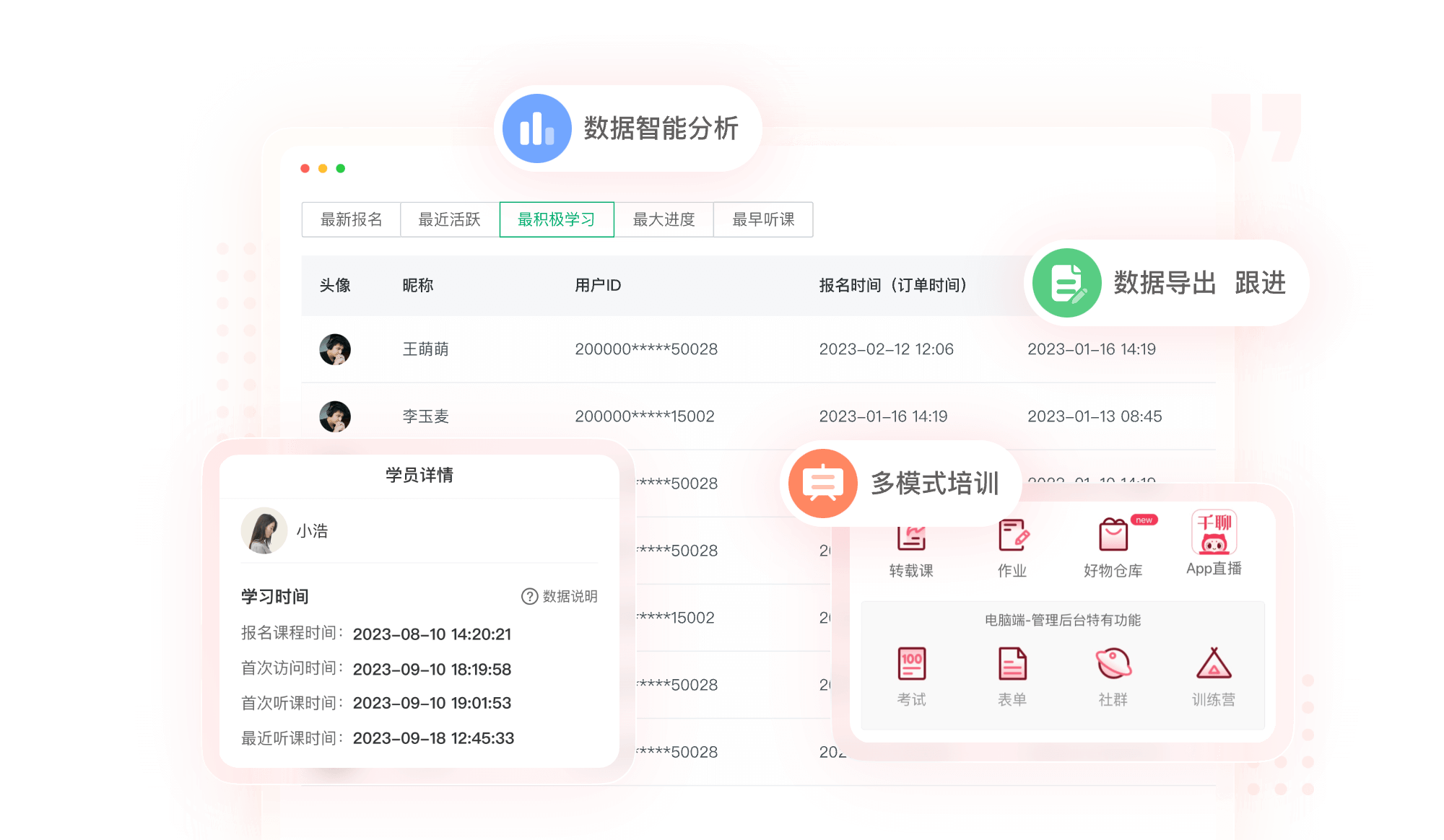
企业培训解决方案:
数字化培训,快速搭建企业大学
多模式培训
支持用图文、音频、视频等形式进行实时直播培训,直播回放方便后续培训实习
互动工具
题库、考试、签到等工具帮助学员巩固知识,提高培训效果
可视化分析
实时查看全员学习情况、课程数、考试分数等数据结果
了解详情
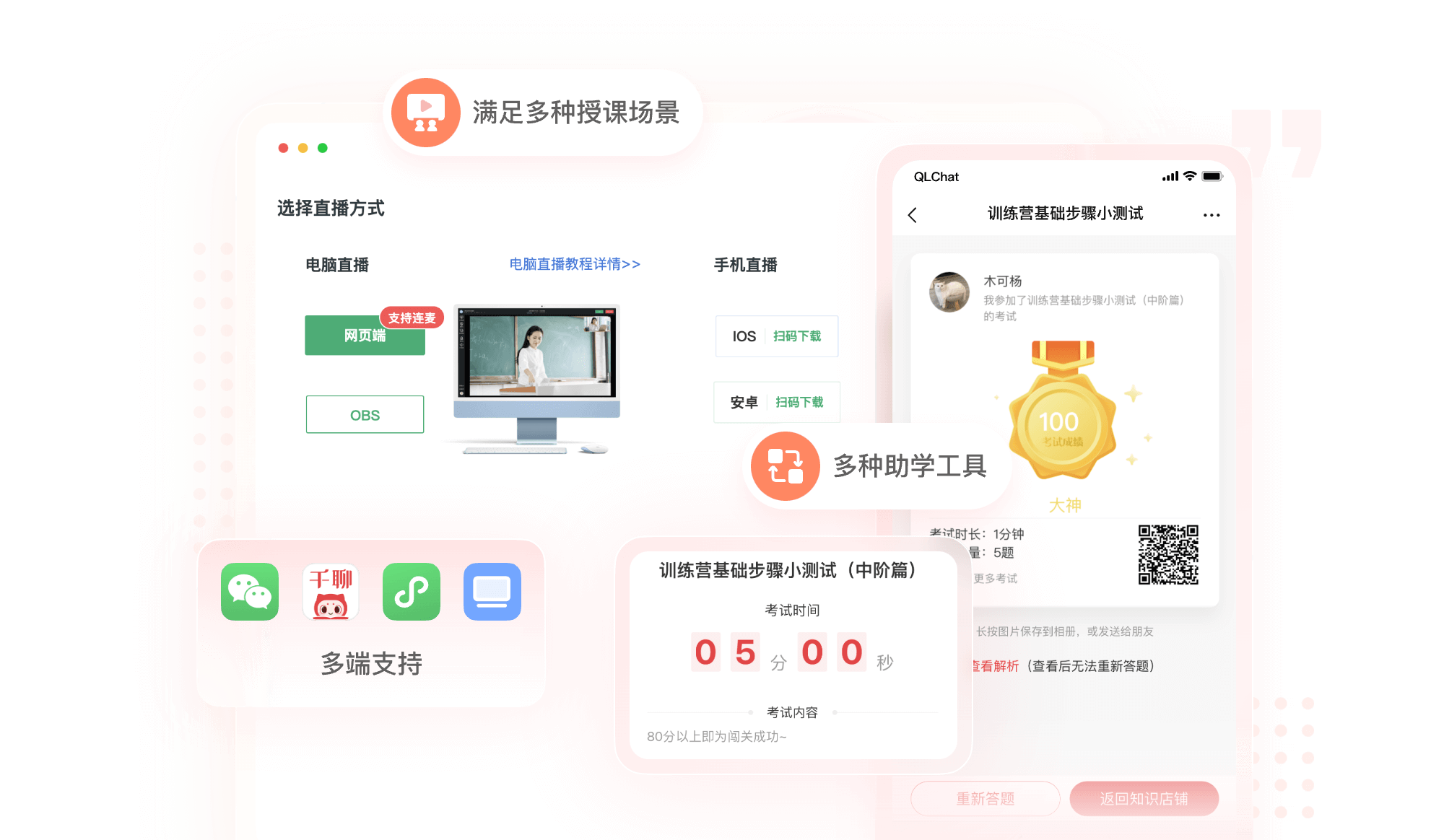
教育培训解决方案:
全方位解决教培机构招生、运营、管理难题
个性化教学
支持专栏、图文、视频、音频、直播授课,满足多种教学场景
课堂互动
签到、考试、作业等工具,深入教、学、练、测、评每个环节,提升教学效果和质量
了解详情
覆盖全渠道知识变现场景
占据全网流量入口
一站式解决全部需求,更合适每个知识从业者的知识付费工具
抖音直播/短视频一键挂载
无需资质审核
即看即买,转化更高
快手直播/短视频一键挂载
无需资质审核
即看即买,转化更高
上架选品中心,课程高曝光
百亿流量扶持
即看即买,转化更高
无需ICP备案
一键转发至微信群/私聊
即开即用
可嵌入公众号
易传播
听课体验感更佳
支持倍速播放
支持电视投屏
无需开发
十大课程形式,支持搭配组合,搭建你的内容体系
视频录播
支持有互动、无互动形式
互动录播
仿直播模式,可提前上传视频,定时播放,节省重复授课时间
开课后学员才可观看视频,直播中无法拖动进度条
支持互动发言:讲师发放多种文件形式教程,学员发言可上墙
无互动录播
无开课时间限制,观众购买后随时收听
方便学员观看系列视频,便捷切换
视频直播
支持半屏直播 、全屏直播
直播授课,支持手机直播、电脑屏幕共享、PPT共享、多镜头等
实时互动性强,弹幕互动:讨论、提问、红包、打赏、购买、分享
公示板区域支持自定义样式,灵活配置邀请有奖、签到任务等
热销导购区支持自定义链接,上架课程、实物商品、优惠券等
半屏直播
支持互动发言:讲师发放多种文件形式教程,学员发言可上墙
语音录播
支持有互动、无互动形式
互动录播
仿直播模式,可提前上传音频,定时播放,节省重复授课时间
开课后学员才可收听音频,直播中无法拖动进度条
支持互动发言:讲师发放多种文件形式教程
弹幕、上墙:边听课边看讨论,精选发言支持上墙常显
无互动录播
无开课时间限制,听众购买后随时收听
方便学员收听课程,界面简洁,操作方便
语音直播
支持有PPT和无PPT形式
直播+语音授课,兼容文字/图片/短视频/文件/图文卡等多种形式
实时互动,支持弹幕、红包、打赏、点赞、提问上墙、签到、考试
文件发送,支持word/ppt/excel/pdf多种文件,并可设置付费收看
多人协作直播下,更多功能拓展,可支持邀请嘉宾、主持人
PPT直播
支持互动发言:讲师发放多种文件形式教程,学员发言可上墙
图文阅读
易分享
无论电脑/手机/平板,图文形式阅读便捷,更易分享传播
短视频
引流路径灵活设置
支持关联自定义链接,自动弹出推广卡片,引导用户点击进入详情页面
分享链接自定义
短视频分享标题、文案、封面支持自定义,提升分享链接转化率
公众号关联
除点赞、评论、分享等操作,也支持引导关注服务号沉淀私域
训练营
通知触达更便利
支持引导添加微信、公众号,收集学员报名信息,对学员精细化运营
多种助学工具
整合作业、课表、社群、打卡等工具,全方位满足定制计划式学习
学员数据跟踪
支持查看学员打卡数据、课程数据,满足强督学式学习的需求
多重方式保护原创内容,减低盗版风险
覆盖教育培训、自媒体、企业内训、内容电商、学校等众多领域

算法加密
对视频进行算法加密,任何未经授权的人都难以破解或下载。保证视频的安全性,有效地杜绝视频被破解和下载的可能性
技术防御
搭配防录屏、防盗播、防篡改,实现从视频源、传播途径、播放终端的多方位技术防御
覆盖多端
覆盖网页/APP/小程序多终端。在不同终端上进行视频播放,都能起到有效保护和管理
超能力护航,安全稳定可靠系统支持
强大的技术实力,多云技术服务支持,多重保障系统稳定和数据安全
 质量管理体系认证证书
质量管理体系认证证书
 高新技术企业
高新技术企业
以用户为中心的陪伴式服务
围绕用户提供「咨询—指导—赋能」全周期1V1的陪伴式服务

各行各业都能免费用上的知识变现工具
满足更多行业的知识变现和线上培训需求
copyright C 2016-2017 www.qlchat.com inc. All Right Reserved 广州思坞信息科技有限公司 版权所有










 质量管理体系认证证书
质量管理体系认证证书
 高新技术企业
高新技术企业
































